
Computing the Multiplicative Inverse for Optimizing Integer Division
|
|
Home |
 |
Back To Tips Page |
 |
Computing the Multiplicative Inverse for Optimizing Integer Division |
|
One of the interesting problems about reverse-engineering code is the rather strange transitions and optimizing compiler can do. Perhaps one of the strangest transformations is the optimization of division by a compile-time constant integer. Because integer division is one of the slowest operations in the computer, the performance is tremendously improved if the division can be done by other means. The simplest solution comes about when the divisor is a power of 2, because then it can be done by a shift (but this is not quite right in general, and doesn't work for signed division without special provision, more on this later). But you can also optimize division by any other integer divisor by computing a multiplier and shift value to perform the actual division.
The trick is to represent the multiplier as a binary fraction. When you multiply a 32-bit integer times the binary fraction, you get a 64-bit result, whose high-order 32 bits are the quotient and the low-order 32 bits are the remainder. For example, to divide a signed integer by 13, the following code does the job:
| Divisor | Dividend | Code |
|
13 |
[esp+4] |
mov eax, 1321528399; 4ec4ec4fH imul DWORD PTR [esp+4] sar edx, 2 mov eax, edx shr eax, 31 add eax, edx |
So where did that strange multiplier come from? Well, the algorithm is given in http://www.hackersdelight.org/HDcode/magic.c, and essentially this code computes the values a and sh such that
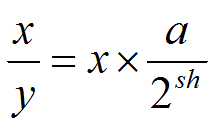
While normally there is no advantage to computing this value at runtime, if you are about to do a tight, intense computation where you don't have a compile time constant divisor, it will make the runtime loop run substantially faster (perhaps an order of magnitude to a factor of 50). The file magic.cpp in the downloadable project contains this algorithm, so you can easily incorporate it into your project.
The value a is referred to in this essay as the multiplicative inverse.
In the pattern shown above, there are two components: the division algorithm, and the sign-compensation algorithm. The first three lines of code are the division algorithm, and the parameters can be found by using the downloadable program attached, as shown:
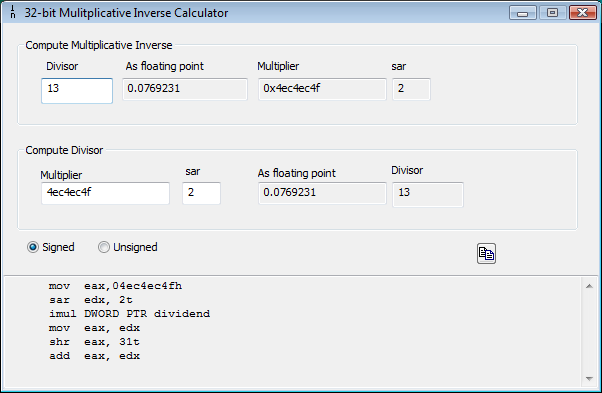
Typing the divisor into the top left box computes the multiplier and sar instruction value. Typing the multiplier found it a piece of code, as an 8-digit hex number, into the lower left box, and giving the sar value, will reveal the original divisor. Note that these are automatically filled in when the divisor is typed into the top left box.
After the imul instruction, the result of eax * 0x4ec4ec4f is found in edx:eax.
The remaining three instructions deal with keeping the value correct if the dividend is negative. The value will be one too high if the result is negative; therefore, the value is adjusted by 1 if it is negative. This is done by shifting the quotient (edx) right by 31 bits using a logical shift right (shr instruction). The result is 0 if the value is positive and 1 if the value is negative. By doing the add instruction, the quotient is adjusted according to the sign bit, and left in eax.
Division in signed or unsigned arithmetic is available. Note that in some cases, the multiplicative inverse is identical in both signed and unsigned arithmetic; in other cases, it can be quite different.
Clicking the copy button (![]() ) will place the entire contents of the edit control
to the clipboard.
) will place the entire contents of the edit control
to the clipboard.
Note that for any given code example, the source value and the result register may be different. In this particular case, the dividend was in [esp+4] and the intended result register is eax. The code generator just refers to the abstract operand dividend. You may substitute your operand source, such as [esp+4], or use the TEXTEQU to define a replacement, e.g.,
dividend TEXTEQU [esp+4]
The basic trick here is to treat the multiplier as the fractional part of a fixed-point integer value. The high-order 32 bits are the integer part, and the low-order 32 bits are the fraction part. Because we normalize the result so there is only a fraction part, we can work with two 32-bit values, but the theoretical 64-bit representation is given as
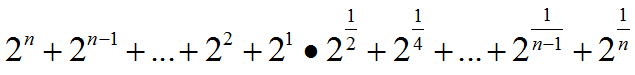
where the high-order value has 32 bits and represents the integer, and the low-order 32 bits represents the fraction, and the bits are interpreted as inverse powers of 2. Unlike a floating point number, the number is not represented with a "hidden" implicit 1=bit. The divisor is normalized to a 4-bit normalization, and the shift constant sh derived in the formula above is the additional factor to be used to compensate for the normalization. The inverter program computes the low-order 32-bit value of the number expressed in the above formula, becaue the integer part is always treated as being 0.
Division of an integer by a power of 2 is trivial; just shift right. To divide by 2n, shift right n bits. Well, only if the integer is positive. As we saw above, there has to be code to compensate for the sign bit. For example, to divide by 4, you would think that a sar 2 would do the job. But in signed arithmetic, it doesn't.
So the code below will handle this:
cdq
and edx, 3
add eax, edx
sar eax, 2
The dividend is placed in the eax register. It is then sign-extended into the edx register by the cdq instruction. The value 2n-1 is computed as a bit mask, and the low-order bits of the sign extension are masked off. This produces a "rounding" value which is either 0 or a sequence of 1-bits equal in length to the shift distance. This value is added to eax and then the shift by n bits to do the division by 2n.
To simplify the discussion, we will show only the low-order 8 bits, where the high-order bit is the sign bit. The values are 2's complement. So if I show 1110 1001, the actual value was 1111 1111 1111 1111 1111 1111 1110 1001. The computation shown here is -23/4, which should be -5. Suppose I do 23/4; the expected result is 5.
However, if we just do a shift right by 2 bits, and the dividend is negative, we get the erroneous computation
We fix this by adding the three instructions shown; one to get the sign value, two more trivial ones to do the rounding, and then the actual shift right, illustrated in detail below.
|
Instruction |
edx |
eax |
|
|
Binary |
Decimal |
||
|
Input state |
???? ???? |
1110 1001 |
-23 |
|
cdq |
1111 1111 |
1110 1001 |
-23 |
|
and edx, 3 |
0000 0011 |
1110 1001 |
-23 |
|
add eax, edx |
0000 0011 |
1110 1100 |
-20 |
|
sar eax, 2 |
0000 0011 |
1111 1011 |
-5 |
For unsigned divide, a logical shift right (shr) of the dividend will suffice. An unsigned divide-by-8 would be simply
mov eax, dividend shr eax, 3t
The source code for the Multiplicative Inverse Calculator can be downloaded. It is a Visual Studio 2008 project.
| Alverson, Robert, “Integer Division Using Reciprocals” (1991) http://citeseerx.ist.psu.edu/viewdoc/summary?doi=10.1.1.33.1710 | |
| Granlund, Torbjörn and Montgomery, Peter, L., “Division by Invariant Integers Using Multiplication” (1994) http://citeseerx.ist.psu.edu/viewdoc/summary?doi=10.1.1.1.2556 | |
| From Hacker’s Delight, (Addison Wesley, 2003) [Note: some browsers will show the code unformatted as a single big block; you will have to reformat it] | |
| http://www.hackersdelight.org/HDcode/magic.c | |
| http://www.hackersdelight.org/HDCode/magicu.c | |
| http://www.hackersdelight.org/divcMore.pdf | |
![]()
The views expressed in these essays are those of the author, and in no way represent, nor are they endorsed by, Microsoft.